During the last decade of his life (1965-1975), Crockett Johnson devoted his time to creating abstract geometrical paintings, all of them based on mathematical theorems. According to his article “On the Mathematics of Geometry in My Abstract Paintings” (1972), Johnson began this work in 1961 “upon belatedly discovering aesthetic values in the Pythagorean right triangle and Euclidian geometry” (97). In all, he painted over 100 canvases, eighty of which are held by the Smithsonian Institution‘s National Museum of American History, Division of Information Technology and Society. Of the remaining paintings, some are privately held and others have been lost.
The Mathematics Division of the Smithsonian’s National Museum of American History has created an on-line exhibit of its eighty Crockett Johnson’s paintings. The website includes not only images, but explanations of the mathematics behind the paintings.
To learn more about Crockett Johnson’s art, see:
- J. B. Stroud’s “Crockett Johnson’s geometric paintings,” in the Journal of Mathematics and the Arts 2.2 (June 2008), pp. 77-99. The article — the most detailed mathematical analysis of this artwork— reproduces 17 of Johnson’s paintings in black and white. The back of the journal reproduces all 11 of these in full color. Highly recommended.
- Stephanie Cawthorne and Judy Green’s “Harold and the Purple Heptagon,” in Math Horizons (Sept. 2009), pp. 5-9.
- Eric Grundhauser’s “The Artful Precision of the Creator of ‘Harold and the Purple Crayon’” (Atlas Obscura, 16 June 2017) mixes good information with many errors, including two in the first sentence.
Below, you’ll find a few of Johnson’s paintings; for a more complete bibliographic listing, see the “Art” section of the Bibliography. To see a larger image of most paintings below, please click on them. Excepting Division of a One-by-Two Rectangle by Conic Rectangles, Projections of Aligned Triangles, and Square Divided by Conic Rectangles, all photos on this page were taken by Philip Nel. Thanks to J. B. Stroud for identifying the titles of Transcendental Curve (Wallis), Problem of Delos (Meneachmus), and Fraction of Pi (to .0000003…) in a Square of One (Tsu Chung Chih). To see images of all eighty paintings held by the Smithsonian, click on the relevant words in this sentence.
Oil on pressed wood, 41 x 24 in. Photo: J. Curtis, Norwalk, CT.
From Visual Art, Mathematics and Computers (Pergamon Press, 1979), edited by Frank J. Malina, p. 306.
48 x 48 in. (excluding frame).
Photographer unknown.
16 x 24 1/2 in. (excluding frame).
12 x 23 1/2 in. (excluding frame).
37 3/4 x 47 3/4 in. (excluding frame).
(Construction of the 113:355 Ratio of Tsu Chung Chih, 500 AD).
23 1/2 x 23 1/2 in. (excluding frame).
47 7/8 x 48 in.
The visual version of Johnson’s theorem.
48 x 42 in.
23 3/4 x 23 3/4 in. (excluding frame).
Photographer unknown.
In December of 1999, I noticed Projections of Aligned Triangles and Square Divided by Conic Rectangles at The Modhaus (“an online gallery of unique furnishings and decorative artifacts from the 1950s-1970s”). I had linked to both paintings (Projections of Aligned Triangles and Square Divided by Conic Rectangles); however, since both are no longer visible at the Modhaus site, you can instead see them above.
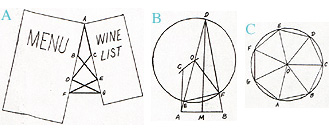
B. Johnson’s construction for a regular heptagon using a compass and straightedge with one mark. Angle EDF measures 180/7 degrees, EOF measures 360/7 degrees, and line segment EF is one side of a regular heptagon.
C. ABCDEFG is a regular heptagon, with each central angle measuring 360/7 degrees.
Johnson’s Cafe Construction for the Heptagon.
J. B. Stroud’s diagram and text from “Stroud studies Crockett Johnson’s mathematical artistry” (1985), an unpublished article which forms the basis of the published “Crockett Johnson’s geometrical paintings” (2008), referenced above.
23 3/4 x 16 in. (excluding frame).
In 1973, when Crockett Johnson was visiting Syracuse, Greece, he sat in an outdoor cafe, rearranging toothpicks at his table. Turning his menu and wine list so that they formed the two equal sides of an isosceles triangle, he placed the toothpicks in a criss-cross pattern across the space in between these two sides (figure 1). Johnson then hypothesized that the angle where the menu and wine list intersected would be 180/7 degrees (“Stroud studies…” 7). His supposition was correct. So what? Well, as Professor J. B. Stroud has shown, this discovery permitted Johnson to “construct a regular seven-sided figure using a compass and straitedge with only one mark on it.” Stroud, the former chair of Davidson College’s Math Department, adds, “As far as I know, nobody thought of trying this until Crockett Johnson. […] The details of how he did it are high school mathematics, but it’s not trivial. It’s darn clever” (“Stroud studies…” 7). When Johnson returned to his studio in Westport, Connecticut, he turned his discovery into art, painting Heptagon from Its Seven Sides (1973).
All of Johnson’s text and artwork is © by the Ruth Krauss Foundation. The rest of these pages are © 1998-2022 by Philip Nel.
